计数排序、桶排序和基数排序
三种线性排序算法 计数排序、桶排序与基数排序 - BYVoid 这篇也说得比较好。 基于比较的排序有快排,插入排序和选择排序等,基于比较的排序算法是不能突破 O(nlogn) 的。
N个数有N!个可能的排列情况,也就是说基于比较的排序算法的判定树有N!个叶子结点,比较次数至少为log(N!)=O(NlogN)(斯特林公式)。
非基于比较的排序,如计数排序,桶排序和基数排序,则有严格的条件限制。
从整体上来说,计数排序,桶排序都是非基于比较的排序算法,而其时间复杂度依赖于数据的范围,桶排序还依赖于空间的开销和数据的分布。而基数排序是一种对多元组排序的有效方法,具体实现要用到计数排序或桶排序。 相对于快速排序、堆排序等基于比较的排序算法,计数排序、桶排序和基数排序限制较多,不如快速排序、堆排序等算法灵活性好。但反过来讲,这三种线性排序算法之所以能够达到线性时间,是因为充分利用了待排序数据的特性,如果生硬得使用快速排序、堆排序等算法,就相当于浪费了这些特性,因而达不到更高的效率。 在实际应用中,基数排序可以用于后缀数组的倍增算法,使时间复杂度从O(NlogNlogN)降到O(N*logN)。线性排序算法使用最重要的是,充分利用数据特殊的性质,以达到最佳效果。 — BYVoid
Swift 使用的排序算法
swift/Sort.swift at master · apple/swift · GitHub
Swift 使用 Timsort - Wikipedia排序算法,Timsort 排序是插入排序和归并排序一起混用的排序算法。 归并排序最好,最坏和平均情况下的时间复杂度都是 O(nlogn) 。而 Timsort 在最好情况下可以达到 O(n) 。Timsort 具体的原理可以看这里 Timsort原理学习 · Sika
二分查找
Redis 的跳表实现
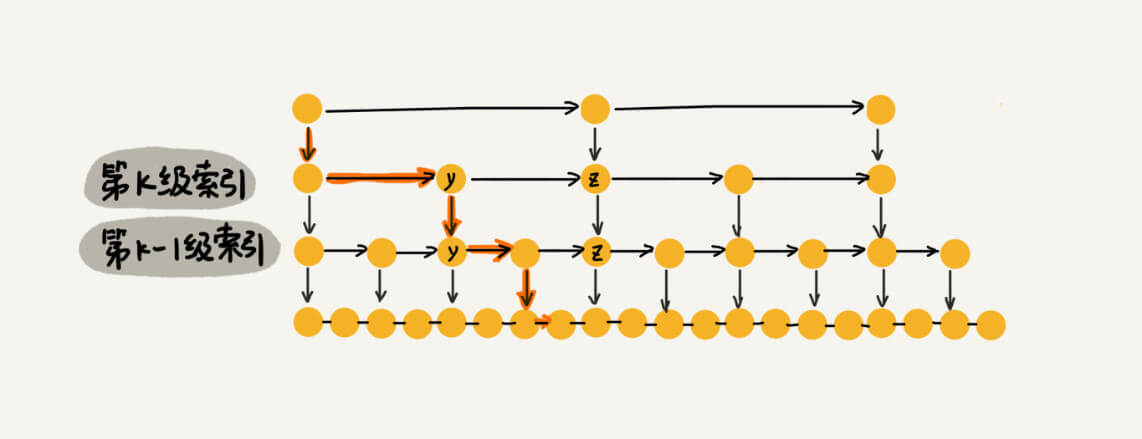
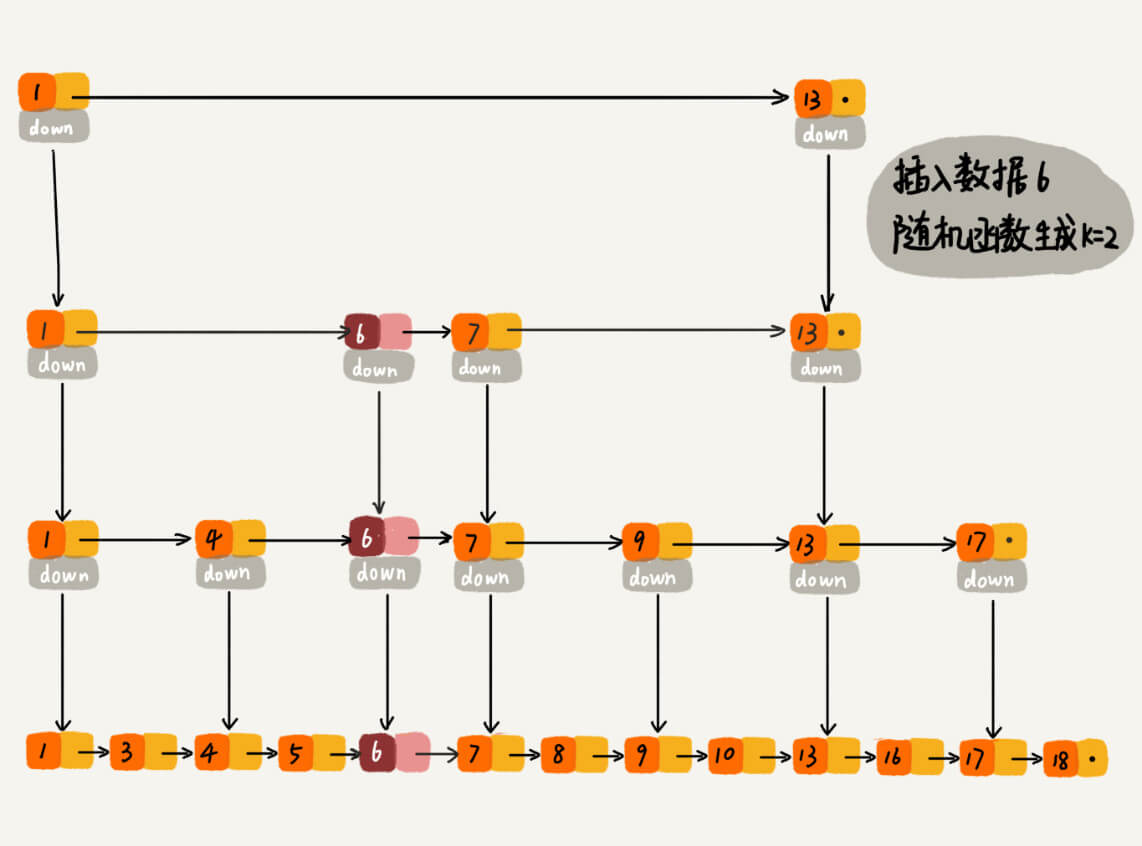
为了提高链表的遍历速度,跳表使用了多级索引来协助查找数据,使得链表查找数据的时间复杂度为 O(n) 。同时链表天生支持高效的插入,删除。为了防止跳表退化成单链表,会在插入时会随机插入部分索引层中。
散列表
散列表是数组的变型,支持数组按照下标随机访问数据的特性,下标就是散列表的 key ,key 通过散列函数 hash(key) 转换成数组下标,再通过下标得到对应的值。散列函数得到的值叫做 Hash 值。
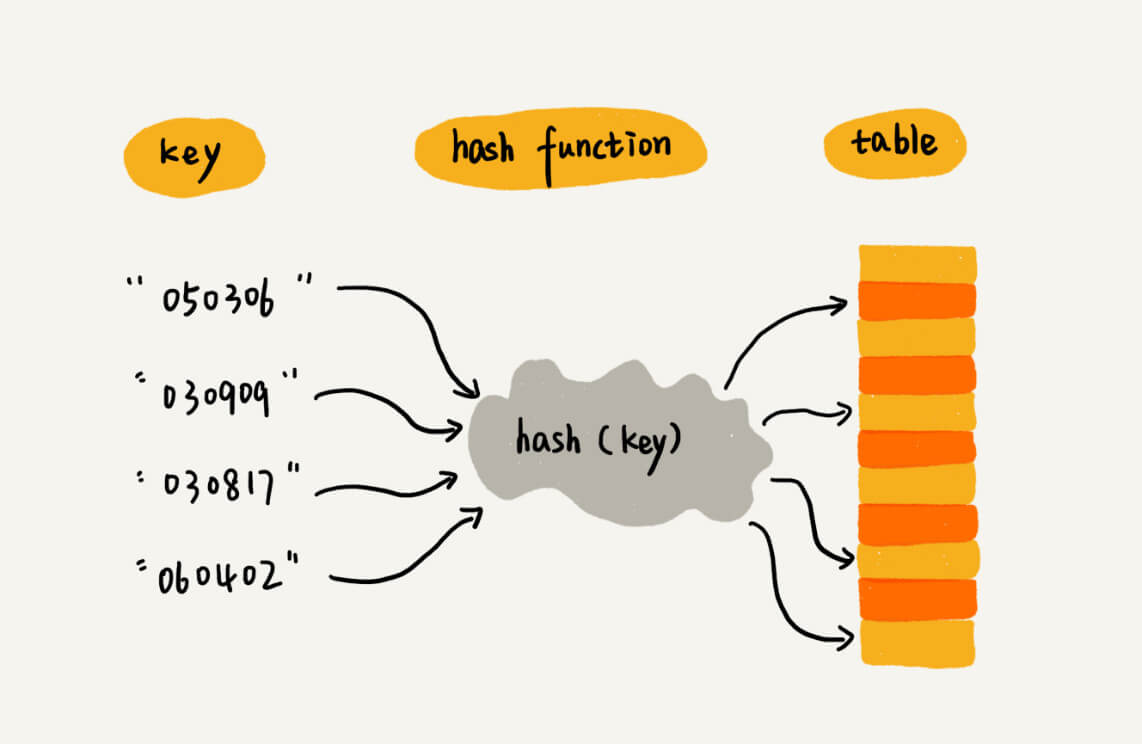
散列函数的设计不能太复杂。过于复杂的散列函数,势必会消耗很多计算时间,也就间接的影响到散列表的性能。其次,散列函数生成的值要尽可能随机并且均匀分布,这样才能避免或者最小化散列冲突,而且即便出现冲突,散列到每个槽里的数据也会比较平均,不会出现某个槽内数据特别多的情况。
装载因子用表示已占据位置的百分比:
1
散列表的装载因子=填入表中的元素个数/散列表的长度
当散列表的元素越多,装载因子就越大,需要进行动态扩容。与数组的扩容不同,散列表的扩容,数据搬移操作需要重新计算每个数据的存储位置。但是可以均摊到每次插入操作里,使得插入操作的时间成本为 O(1) 。如果内存紧张,还可以使用动态收缩,同时也可以根据情况调整装载因子的大小。
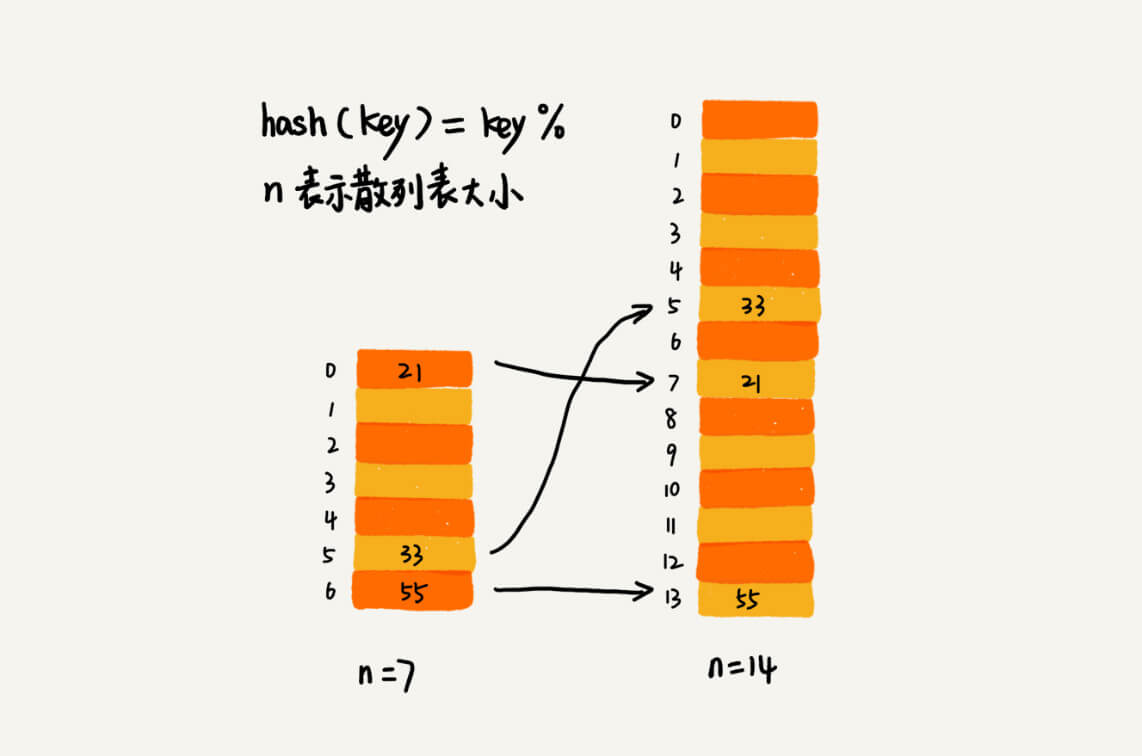
为了避免一次性扩容时耗时过多,可以讲数据搬移操作分摊到后续的插入操作中,每次插入数据时都对旧的数据进行一次搬移操作。
解决冲突
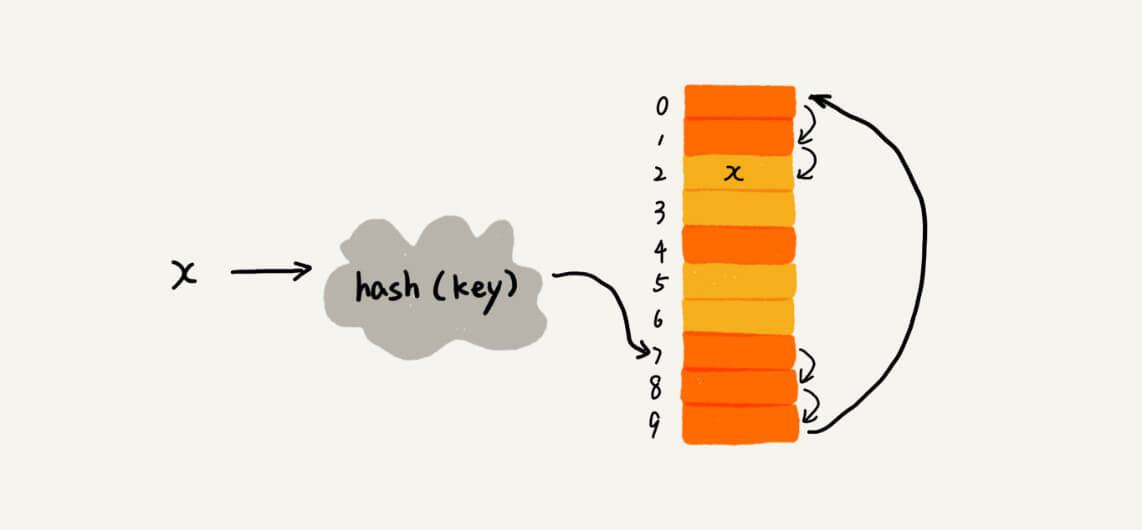
开放寻址法
开放寻址法的核心思想是,如果出现了散列冲突,就重新探测一个空闲位置,将其插入。探测方法有线性探测,二次探测和双重探测等。 优点:
- 所有数据都在数组中,有效利用 CPU 缓存加快查询呢速度;
- 序列化比较简单
缺点:
- 处理冲突的代价更高,所以装载因子的上限不能太大,导致需要更多的内存工具;
链表法
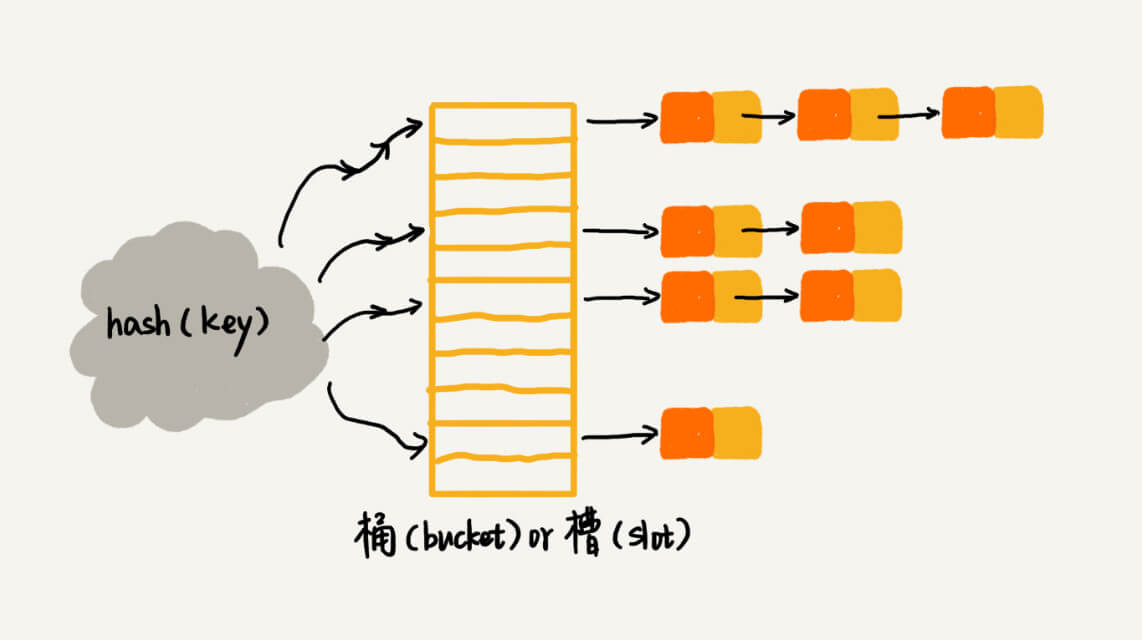
链表法是一种更加常用的散列冲突解决办法,在散列表中,每个“桶(bucket)”或者“槽(slot)”会对应一条链表,所有散列值相同的元素我们都放到相同槽位对应的链表中。链表需要存储指针,会消耗额外的内存,且不是连续的内存分布,对 CPU 缓存不友好。基于链表的散列冲突处理方法比较适合存储大对象、大数据量的散列表,而且,比起开放寻址法,它更加灵活,支持更多的优化策略,比如用红黑树代替链表。
使用 Swift 来实现 Hash Table ,采用的是链表法,Hash Table 。
散列表和链表结合一起可以使增删改查操作都在 O(1) 时间内完成。
Comments powered by Disqus.